Diseñar un circuito lógico que active una sirena aplicado a un sistema de riego.
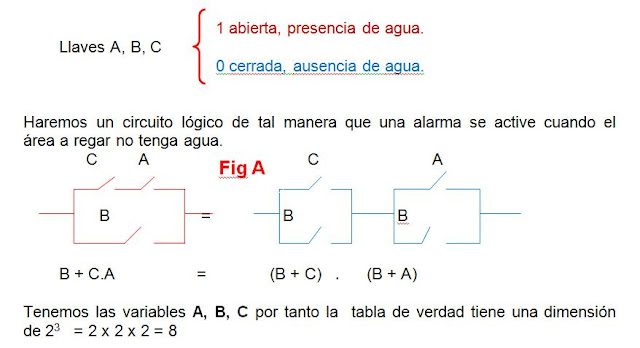
El sistema de riego de la figura requiere de un diseño lógico que permita activar una alarma, para una combinación particular del estado de las llaves A, B y C y que haya la posibilidad de que el sistema se quede sin agua.
La convención a usar para indicar que una compuerta está abierta y que la alarma está activada es la siguiente:
Alarma = 1; Alarma activada.
Alarma = 0; Alarma apagada.
A = 1; Compuertas A abierta.
A = 0; Compuertas A cerrada
Igual para las compuertas B y C.
El proceso de diseño debe contar con las siguientes etapas:
1. Descripción analítica del problema a resolver, declaración de variables, definición de la dimensión de la tabla de verdad.
Se tienen tres llaves A, B y C, en un sistema de regadío, las que al abrir suministran liquido, para tal caso su valor lógico es 1, cuando las llaves están cerradas su valor lógico es 0, y por tanto no hay suministro de liquido.
Como se cuentan con tres llaves se originan 8 combinaciones posibles, donde cualquiera de ellas puede tomar los valores abierto o cerrado. Lo que no se desea es que las llaves A y B se encuentren cerradas al tiempo, porque el sistema se queda sin agua, para tal caso se debe activar una alarma que corresponde a la variable de salida F.
La llave C esta montada en el sistema como llave de paso y no de salida pero el valor que tome afecta también a la salida F.
2. Tabla de verdad con los posibles estados de las compuertas.
3. Función lógica expresada en forma normal conjuntiva.
La forma normal conjuntiva esta en relación con los ceros.
F=(A+B´+C) (A+B´+C´) (A´+B+C´) (A´+B´+C) (A´+B´+C´)
4. Circuito lógico derivado de la forma normal conjuntiva.
5. Función lógica expresada en forma normal disyuntiva.
La forma normal disyuntiva está formada por los unos de la salida.
F=A´B´C´+A´B´C+AB´C´
6. Circuito lógico derivado de la forma normal disyuntiva.
7. Función lógica simplificada a partir de la forma normal disyuntiva.
F=A´B´C´+A´B´C+AB´C´
F= (A´B´C´+A´B´C) + (A´B´C´+AB´C´)
F=A´B´ (C´+C) + B´C´ (A´+A)
F=A´B´ (1) + B´C´ (1)
F=A´B´+B´C´
8. Función lógica simplificada usando mapas de Karnaugh.
F=A´B´+B´C´
9. Circuito lógico derivado de la simplificación con mapa de Karnaugh.
Diseño elavorado por Carlos Alberto Goyeneche Alfonso.







El diseño con las puertas me gusta, y lo explicas bien. Sólo un pequeño apunte: procura elaborar con b en lugar de con v
ResponderEliminar